What is Standardization, and why is it important?
In statistics, standardization is placing different variables on an identical scale. This helps you to compare values between different types of variables.
Data gives more meaning when you compare it to something. For example, it’s nice to know that your online product sales have reached 100 people this month, but that doesn’t tell you what you should do next year.
If it’s a 50% decrease from last month, it indicates to improve in your marketing strategy. If this is a 50% increase, you are sure you’re heading in the right direction.
Let’s take this one step more — data comparisons are not helpful if you have data in different scales of units or irrelevant data.
For example, it may be helpful to compare your sales to a certain part of a region where most of the people are online but not in other parts where fewer people are using the Internet.
In this case, both the datasets are on a different measurement scale. Another example could be measuring the price of a product in INR and USD.
Data standardization is the method of ensuring that your dataset can be compared to different data sets. It’s a key part of the research and analysis, and it’s one thing that everybody who uses data for comparison should consider before they even collect, clean, or analyze their first data point.
How to standardize variables?
To standardize variables, you must calculate a variable’s mean and standard deviation. Then, for every variable’s value, you must subtract the mean and divide it by the standard deviation.
Every distribution can be standardized if the mean and the variance of a variable are and
, respectively.
Standardization is the method of transforming a variable with a mean of zero and a standard deviation of 1.
What is Standard Normal Distribution?
A normal distribution can also be standardized. The outcome is called a standard normal distribution.
You could also be questioning how the standardization goes down right here.
Well, all we have to do is just shift the mean by and the standard deviation by
. The letter Z is used to indicate it.
As we already mentioned, its mean is zero and its standard deviation: is 1.
The resultant standardized variable is called a z-score. It is identical to the original variable, minus its mean, divided by its standard deviation.
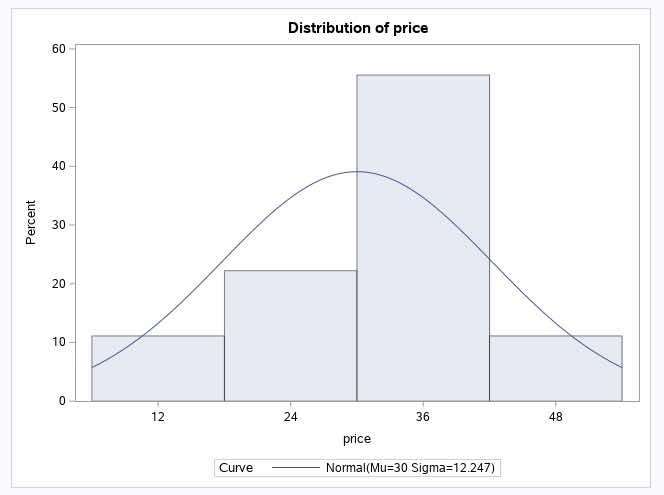
A Case in Point – Let’s take an approximately normally distributed set of numbers:
10, 20, 20, 30, 30, 30, 40, 40, and 50.
Its mean is 30 and its standard deviation: is 12.24. Now, let’s subtract the mean from all data points.
As shown below, we get a new data set of:
-20, -10, -10, 0, 0, 0, 10, 10, and 20.
The new mean is 0, precisely as we anticipated.
On a graph, the curve is shifted towards the left, but it has preserved its shape.
The NEXT step in Standardization…
So far, we now have a new distribution. It remains normal, however, with a mean of zero and a standard deviation of 1.22.
The subsequent standardisation step divides all data points by the standard deviation. This will drive the standard deviation of the new data set to 1. Let’s return to our instance.
The original dataset has a standard deviation of 12.24. This is similar to the dataset we obtained after subtracting the mean from every data point or value.
Adding and subtracting values to all data points doesn’t change the standard deviation.
Now, let’s divide every data point by 12.24. As you can see in the image below, we get:
0.81,1.63,1.63,2.45,2.45,2.45,3.26,3.26,4.08
If we calculate the standard deviation of this new data set, we will get 1.
And the mean remains to be 0! The curve also remains the same, as shown below.
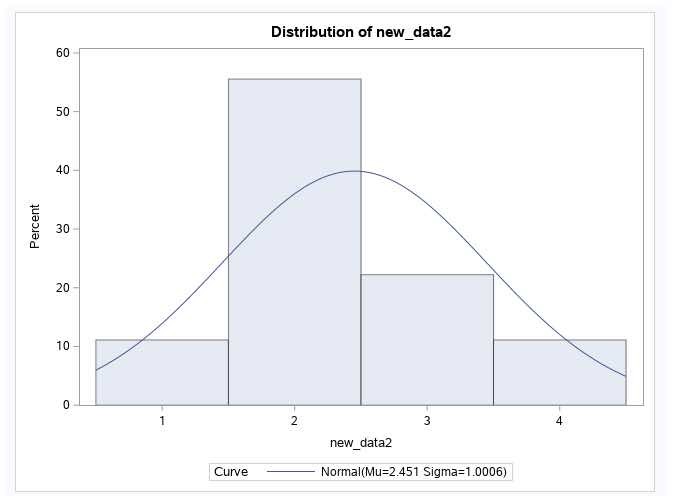
This is how we will acquire a standard normal distribution from any normally distributed data set.
How to Standardize variables in SAS?
Standardizing variables in SAS is very simple using the proc standard procedure below.
PROC STANDARD DATA=product MEAN=0 STD=1 OUT=product2;
VAR price ;
RUN;Key Takeaway
Standardization of variables predictions and inferences of variables is a lot simpler.
For example, a value of 0.5 in a standardized dataset indicates that the value for that observation is half a standard deviation above the mean. In contrast, a value of -2 indicates that it has a value of 2 standard deviations lower than the mean.
The objective of standardizing variables is to ensure all variables contribute evenly to a scale when items are added together, making it easier to interpret the results of regression or other analyses.
If you liked this article, you might also want to read Confidence Interval for Population Mean and Central Limit Theorem.
Do you have any tips to add? Let us know in the comments.
Please subscribe to our mailing list for weekly updates. You can also find us on Instagram and Facebook.


