Basics of Hypothesis Testing

Hypothesis testing is the statistical process of either retaining a claim or belief made by a person that is usually about population parameters such as mean or proportion. We seek evidence from a sample that supports the claim.

Hypothesis testing consists of two statements called the null hypothesis and alternative hypothesis, and only one of them is true.

Hypothesis testing aims to either reject or retain a null hypothesis. In many cases, like in regression models, one would like to reject the null hypothesis to establish a significant relationship between the dependent and the independent variables.

In the Goodness of fit test, which is used for checking whether the data follows a specific distribution or not, we would like to retain the null hypothesis.

Null and Alternate hypothesis

The null hypothesis is denoted as , and it refers to the statement that there is no relationship between distinct groups concerning the values of a proportion parameter.

The null hypothesis is also the claim that is assumed to be true initially and would try to retain it unless there is a piece of strong evidence against the null hypothesis.

Alternate hypothesis is denoted as or . The complement of the null hypothesis is what the researcher believes to be true and would like to reject the null hypothesis.

Test Statistics

Test statistics are the standardized difference between the estimated value of the parameter being tested calculated from the samples and the hypothesis values to establish the evidence supporting the null hypothesis.

The p-value is the conditional probability of observing the statistic value when the null hypothesis is true.

Example:

The average annual salary of Machine Learning experts is at least 100,000. The corresponding null hypothesis is . Assume that the population’s standard deviation is known, and the standard error of the sampling distribution is 5000.

The standardized distance between the estimated salary from the hypothesis salary is (110,000 – 100,000)/5000 = 2. We can now find the probability of observing this statistic value from the sample if the null hypothesis is true. .

A large, standardized distance between the estimated and hypothesis values will result in a low p-value.

p-value corresponding to is shown below.

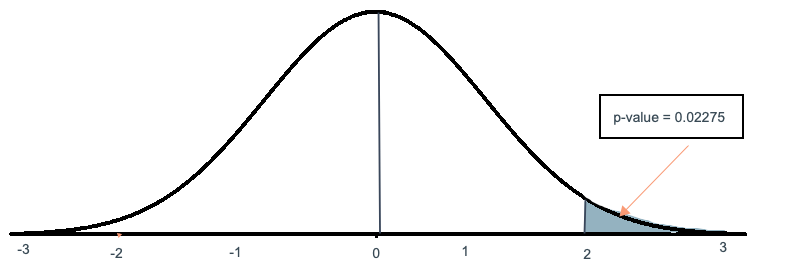
The probability of observing a value of 2 and higher from a standard normal distribution is 0.002275. If the population mean is 1,00,000, and the standard error of the sampling distribution is 5000, then the probability of a sample mean greater than or equal to 1,10,000 is 0.02275.

The value 0.02275 is the p-value, which is the evidence supporting the statement in the null hypothesis.

Significant value

The primary objective in hypothesis testing is to either reject or fail to reject the null hypothesis. Therefore, we need criteria to make a decision.

The significance level is the criteria for deciding the null hypothesis based on the calculated p-value Significance level is denoted by .

The significance value is the maximum threshold for the p-value. The decision to reject or retain will depend on whether the calculated p-value crosses the threshold value of or not.

One-tailed test

One-tailed hypothesis tests are used to test for effects in only one direction. When you perform a one-tailed test, the entire significance level percentage goes into the end of one tail of the distribution.

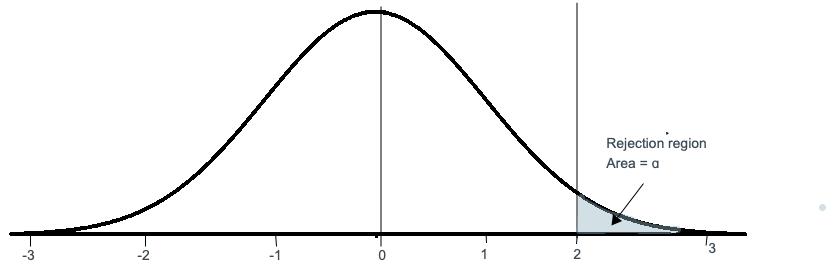
In the examples above, for an alpha value of 5%, each side of the distribution has one shaded region of 5%. When you perform a one-tailed test, you must determine whether the critical region is in the left tail or the right tail.

In a one-tailed test, you have two options for the null and alternative hypotheses, corresponding to where you place the critical region.

You can choose either of the following sets of generic hypotheses:

→ The effect is less than or equal to zero. → The effect is greater than zero.

or

→ The effect is greater than or equal to zero. → The effect is less than zero.

Example 1:

The claim made by an agency in Bangalore is the average disposable income of families living in Bangalore is greater than ₹ 4200 with a standard deviation of 3200. Given sample size is 40000 families, the mean was estimated to be ₹ 4250.

Assuming that the population standard deviation is ₹ 3200. Conduct an appropriate hypothesis test at a 95% confidence level to check the validity of the agency.

The null hypothesis, in this case, is given by

is the average disposable salary. The equality symbol is always part of the null hypothesis since we have to measure the difference between the estimated value from the sample and the hypothesis value.

In this case, rejection or acceptance will depend on the direction of deviation of the estimated parameter value from the hypothesis value. Since the rejection region is only on one side, this is a one-tailed test.

Since the population standard deviation is known, we can use the z-test.

The corresponding z-value at for the right-tailed test is approximately 1.64.

In Excel, you can find this that is NORMSINV(0.95).

We reject the null hypothesis since the calculated z-value is greater than the z-critical value.

The p-value is 0.00088, which can be found using 1-normsdist which is 1-normdist(3.125).

In SAS, you can calculate the p-value by using the CDF function.

data _null_;
p_value=1-cdf('normal',3.125);
put p_value=;
run;

Running a one-sample t-test in SAS.

PROC TTEST is used to perform hypothesis testing in SAS. You can use PROC TTEST on the input dataset (if you have the raw data) or on summary statistics.

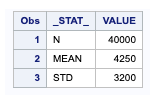
To use PROC TTEST on summary statistics, the statistics must be in a SAS data set that contains a character variable named _STAT_ with values ‘N‘, ‘MEAN‘, and ‘STD.‘

data SummaryStats; 
infile datalines dsd truncover; 
input _STAT_:$8. VALUE; 
datalines; 
N, 40000 MEAN, 
4250 STD, 3200 
;

proc ttest data=SummaryStats sides=U alpha=0.05  h0=4200;
      var value;
   run;

The VAR statement indicates the variable to be studied, while the = option specifies that the mean should be compared to 4200, the hypothesized value, rather than the default of 0.

The SIDES=2 option specifies the number of sides and directions. The other options are U and L

We want to find out whether the mean income is more than 4200. So, the sides =U option is given, which is also the default.

If we have to find whether the mean income is different than 4200, we will use sides=2.

The ALPHA=0.05 option requests a significance level of 0.05 or a confidence level of 95%. The default significance level is 0.05.

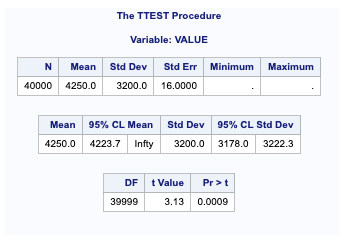
Interpreting the result of the t-test

Summary statistics are displayed at the top of the output. The sample size (N), mean, standard deviation and standard error are displayed with the minimum and maximum values if you use a raw dataset.

The 95% confidence limits for the mean and standard deviation are in the following table.

At the bottom of the output are the test’s degrees of freedom, statistic value, and p-value.

At the 0.05 significance level, this test indicates that the mean income is more than 4200; thus, we would reject the null hypothesis. (t=3.13 and p-value=0.0009 > 0.04).

Two-tailed test

A two-tailed test is a test of a hypothesis where the area of rejection is on both sides of the sampling distribution.

If we use a significance level of 0.05, a two-tailed test shares alpha to test the statistical significance in one direction and the other half in the other. This means that .025 is in each tail of the distribution of your test statistic.

In a two-tailed test, regardless of the direction of the relationship, the objective is to test for the possibility of the relationship in both directions.

NOTE: We should use a one-tailed test only if we have a good reason to expect the difference to be in a particular direction. A two-tailed test is more conservative than a one-tailed test because a two-tailed test takes more extreme statistics to reject the null hypothesis. 

Example:

A passport office claims that passport applications are processed within 30 days of submitting the application form and all the necessary documents. The below table shows the processing time of 40 passport applicants. The population standard deviation of the processing time is 12.5 days.

Conduct a hypothesis test at significance level to verify the claim.

16	16	30	37	25	22	19	35	27	32
34	28	24	35	24	21	32	29	24	35
28	29	18	31	28	33	32	24	25	22
21	27	41	23	23	16	24	38	26	28

Solution:

The null and alternative hypothesis, in this case, is given by

The given estimated sample mean is 27.05 days.

The value of Z-statistics is given by

The critical value of the left-tailed test for is -1.6444.

Since the critical value is less than the Z value, we fail to reject the null hypothesis.

The p-value for z = -1.4926 is 0.06777, which is greater than the value of .

Hence, there is no strong evidence against the null hypothesis.