In SAS, there are several procedures and functions that can be used to calculate confidence intervals, each with its own strengths and limitations.
In this blog post, we will explore different methods for calculating confidence intervals in SAS, including the PROC MEANS, PROC UNIVARIATE, and PROC TTEST procedures. We will also discuss how to interpret the results and make informed decisions based on the level of uncertainty in our data.
A confidence interval is a statistical concept that provides a measure of the degree of uncertainty associated with an estimate of a population parameter. It shows the range of values where the true value of the parameter is likely to fall, with a certain level of certainty.
The sample size, the level of confidence, and how different the data are all affect how wide the confidence interval is.
As the size of the sample or the level of confidence goes up or down, the width of the interval goes down. This means that the estimate of the population parameter is more accurate.
It is important to remember that the confidence interval is a measure of how close the estimate is, not how close it is to the truth.
The estimate may still be far from the true value of the parameter, even if the confidence interval is narrow.
Confidence intervals are a useful tool for interpreting the results of a study and making inferences about the population based on sample data.
Think about a study that tries to find out how tall men in a certain population are, on average.
A random sample of 100 men is selected, and their heights are measured. The mean height of the sample is found to be 68 inches, with a standard deviation of 4 inches.
This means that if the study were repeated many times, 95% of the intervals calculated would contain the true mean height.
This statement means that it is 95% certain that the population proportion of the true mean height of adult men in the population is 67.22 to 68.78.
Can we say that the confidence interval (67.22, 68.78) contains the true population proportion? The answer is unknown.
The population proportion is fixed but has an unknown value. It is important to remember that 95% confidence does not mean 95% probability.
Consider the following…
Statement A: The mean height of the adult men in the population is found to be 68 inches.
Statement B: I am 95% confident that the average height of adult men in the population is estimated to be between 69.40 and 70.80 inches.
Statement B provides us with more information because it not only provides us with a statistic but also tells us how confident we can be in that statistic.
Assumptions
When constructing confidence intervals, it’s important that certain assumptions are met. If these assumptions are violated, then the confidence interval can become unreliable.
Assumptions for Confidence Intervals
Confidence intervals are widely used in statistics and provide a range of plausible values for a population parameter. However, there are several assumptions that need to be satisfied in order to accurately calculate confidence intervals.
- Independence: The observations in the sample should be independent and not related to each other in any way.
- Random Sampling: The sample should be selected randomly from the population to ensure representativeness.
- Normality: The population distribution should be approximately normal. If the sample size is large enough (typically n > 30), then the central limit theorem states that the sample mean will be approximately normal, even if the population is not.
- Equal Variance: The population variances should be equal for each group being compared. If the variances are unequal, then it may be necessary to use a different statistical method, such as Welch’s t-test.
- No Outliers: The sample should not contain any outliers that could significantly affect the results.
- Known Variance: The variance of the population should be known or estimated from the sample data.
It’s important to keep these assumptions in mind when calculating confidence intervals and interpreting the results. If these assumptions don’t hold true, the confidence interval might not show how uncertain the population parameter really is.
Normality test
A normality test is a way to use statistics to find out if a set of data is roughly spread out in the same way.
It compares the distribution of the sample data to the normal distribution and gives a measure of how well the sample data fits the normal distribution. Common normality tests include the Shapiro-Wilk test, the Lilliefors test, the Anderson-Darling test, and the Kolmogorov-Smirnov test.
The choice of normality test depends on the sample size and the distribution of the data.
= Height is normally distributed
= height is not normally distributed
ods graphics on;
proc univariate data=_9to5sas.demog;
var height;
histogram height /normal(mu=est sigma=est);
inset skewness kurtosis;
probplot height /normal(mu=est sigma=est);
inset skewness kurtosis;
run;The normal in the top line requests test statistics for checking normality.
If mu=EST and sigma=EST, SAS will use the sample mean and sample error calculated from the data to be the parameters of the reference straight line.
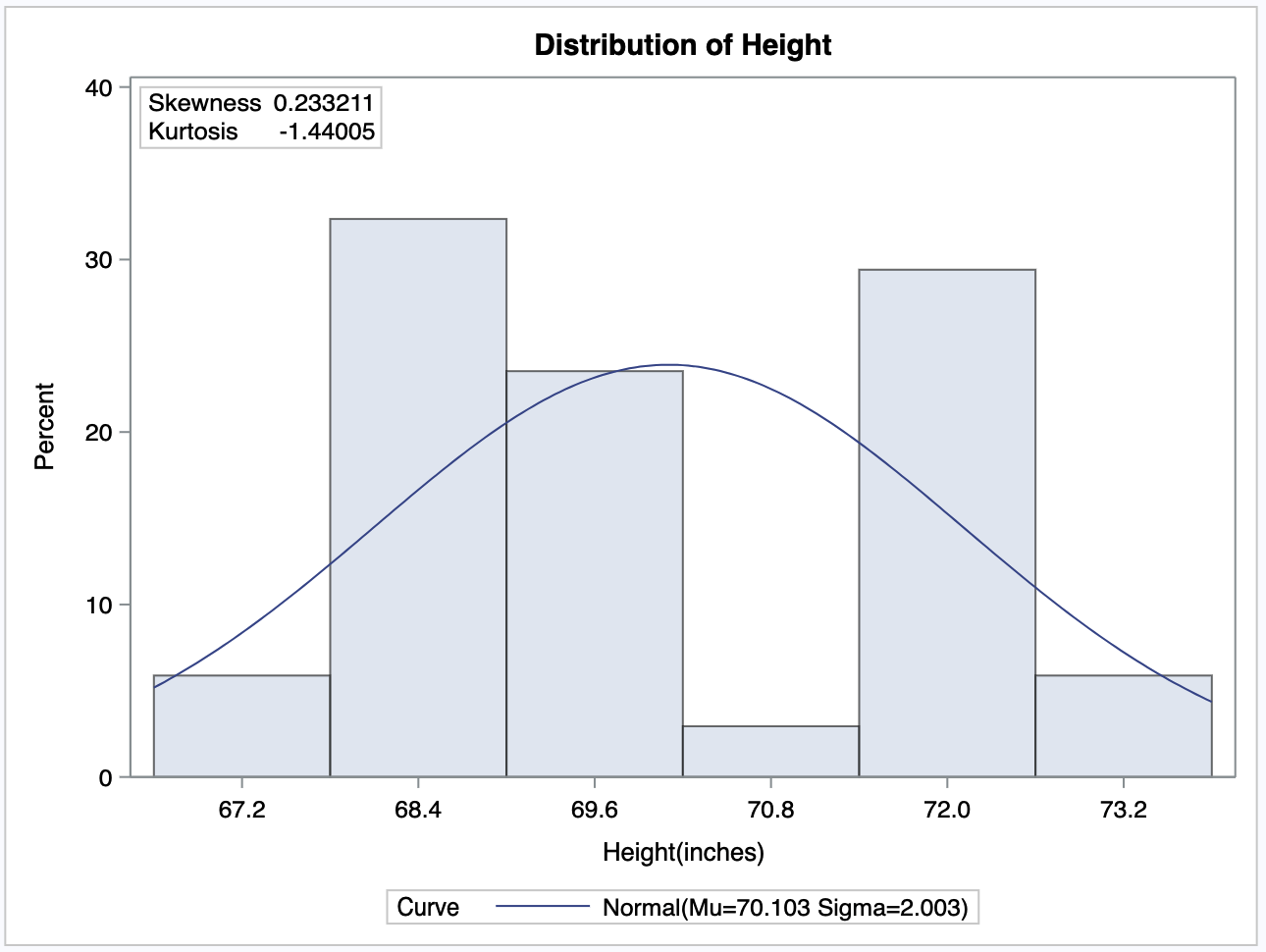
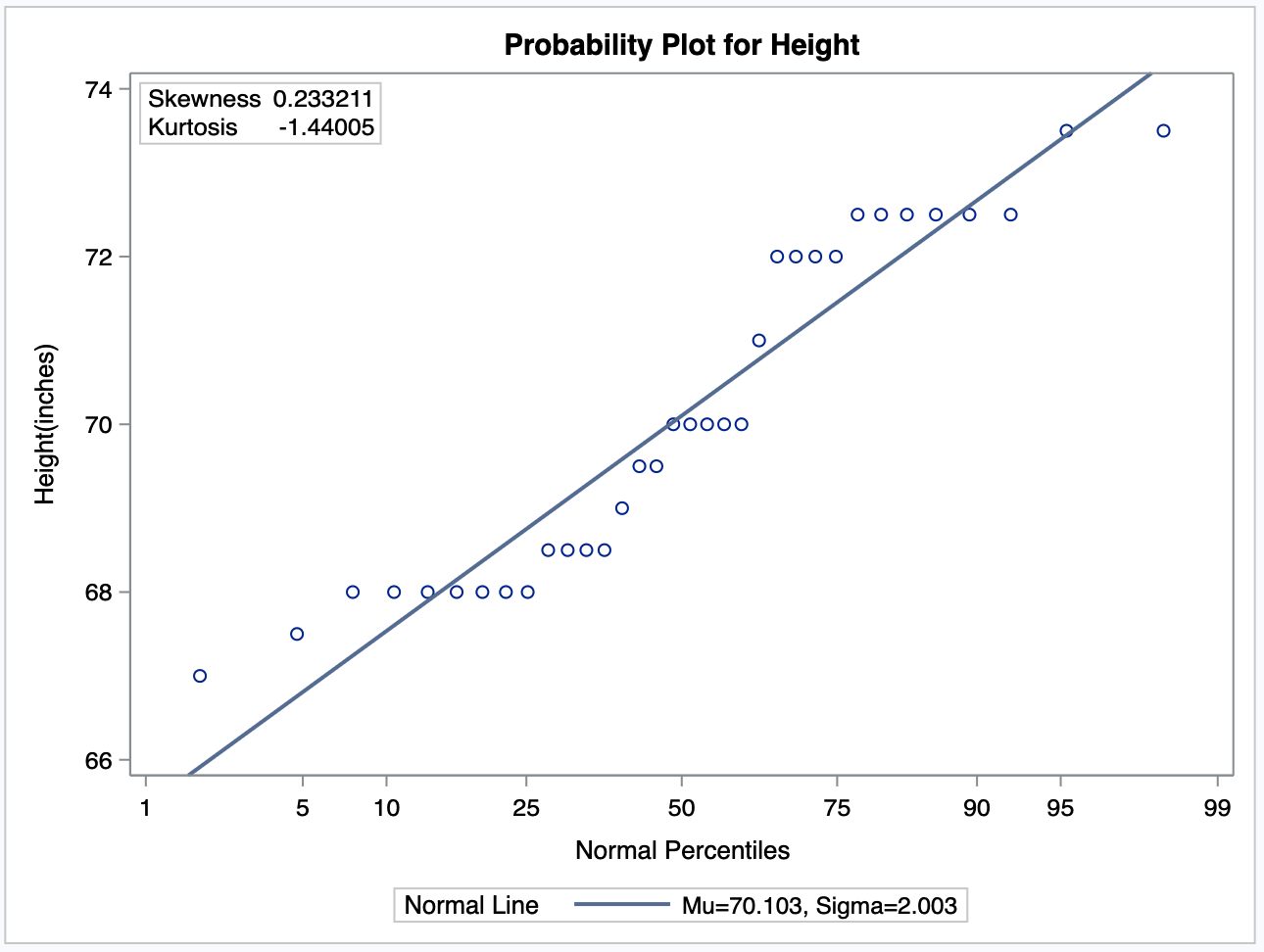
In SAS, a probability plot, also called a quantile-quantile (Q-Q) plot, shows how a sample and a theoretical distribution compare visually.
The plot is used to assess the normality of the data and to determine if it follows a specific distribution.
To create a probability plot in SAS, you can use the PROC UNIVARIATE procedure. For example:
ods select testsfornormality;
proc univariate data=_9to5sas.demog normaltest;
var height;
run;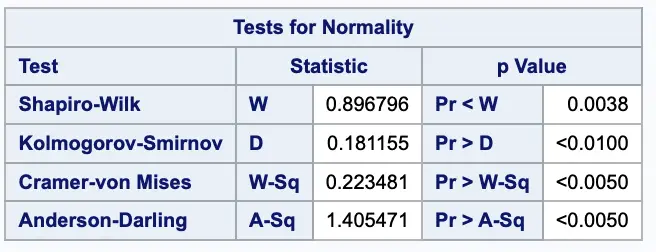
The P value is a measure of the strength of the evidence against the null hypothesis. In this case, the null hypothesis is that the data is normally distributed.
If the P value is less than a significance level, typically 0.05, it means that there is convincing evidence against the null hypothesis, and the data is not normally distributed.
In this case, the P value of 0.0038 is less than 0.05, so we can conclude that the data is not normally distributed. T
his P value suggests that there is a less than 0.38% chance that the data would have this non-normal distribution if the null hypothesis were true.
The probability plot also supports the assumption that the data is not normal.
Using Proc Means to calculate confidence Interval
You can use the SAS procedure PROC MEANS to calculate the confidence interval in SAS.
Run the PROC MEANS procedure to find the mean, standard deviation, and other statistics that describe your data. You can specify the input dataset using the data= option.
In proc means, you can use CLM to get the confidence interval of the mean
In the PROC MEANS procedure, you can use the alpha= option to specify the level of confidence you want to use.
For example, to calculate the 95% confidence interval, you can use alpha=0.95.
proc means data=_9to5sas.demog maxdec=2 n mean max min stddev stderr clm alpha=0.05
nonobs;
var height;
run;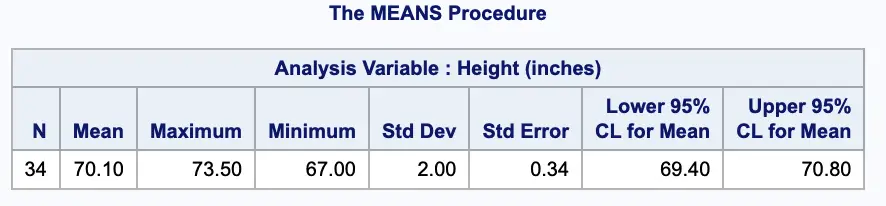
Using Proc Univariate
The UNIVARIATE procedure in SAS can be used to determine confidence intervals using the t-distribution by specifying the CIBASIC option.
By default, SAS gives you a 95% confidence interval. You can find it in the section of the output called “Basic Confidence Limits Assuming Normality.” The confidence level can be adjusted by specifying the ALPHA option.
ods select basicintervals;
proc univariate data=_9TO5SAS.demog cibasic alpha=0.05;
var height;
run;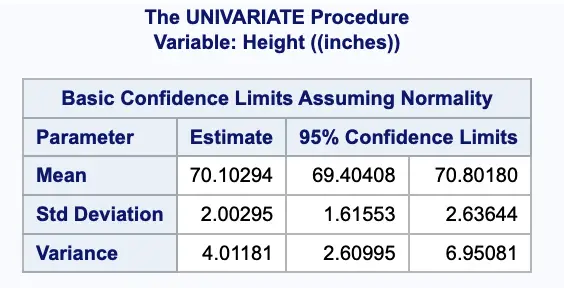
Using proc TTEst
Proc Ttest stands for the t-test procedure. It gives us the confidence interval for the mean.
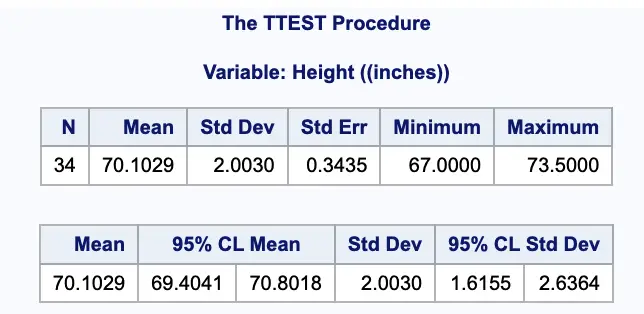
The summary Statistics show the following results.
- Variable – This is the list of variables.
- N – This is the number of valid (i.e., non-missing) observations used in calculating the t-test.
- Mean – This is the mean of the variable.
- Std Dev – This is the standard deviation of the variable.
- Std Err – This is the estimated standard deviation of the sample mean.
- 95% CL Mean – These are the lower and upper bounds of the confidence interval for the mean.
- 95% CL Std Dev- Those are the lower and upper bounds of the confidence interval for the standard deviation.
Conclusion
In conclusion, SAS offers several options to calculate confidence intervals for data analysis.
The most used procedures are PROC MEANS, PROC UNIVARIATE, and PROC TTEST. PROC MEANS and PROC UNIVARIATE are the most straightforward and can be used to calculate the basic confidence interval for normally distributed data. However, PROC TTEST offers more flexibility and can be used for data that is not normally distributed.
When calculating a confidence interval in SAS, it is important to specify the confidence level and the variable of interest. Most of the time, a confidence level of 95% is used, but this can be changed if needed.
The resulting output from the procedure will provide information on the estimate, standard error, confidence interval, and other relevant statistics.
Overall, SAS has powerful ways to analyze data, and calculating confidence intervals is an important part of this. Analysts can learn useful things about their data and come to meaningful conclusions when they follow the right procedure and set the right parameters.



