Most people use Excel to make financial calculations. But SAS is also very capable of helping in finance too. One of the advantages of using these functions is the way it is structured and the possibility of automation.
This article will show some of the most common formulas used in finance.
- PMT: Calculating the monthly payment of a loan
- FV: computes the future value of an investment.
- PV: computes the present value of an investment.
- NPER: Computes the number of periodic payments.
- RATE: Computes the interest rate per period of an annuity.
- PPMT: computes the payment on the principal for an investment for a specified period.
- EFFECT: Computes the effective annual interest rate
- IRR: Computes the internal rate of return for a series of cash flows
- NPV: Computes the net present value
Note: Negative values used in the examples represent payments or cash outflow, positive values represent income, and values of 0 represent no cash flow.
1. Calculating Future Value of an Investment
One dollar put into a savings account today might be worth more than one dollar a year from now.
How does that work? The bank pays interest, and your dollar earns money for that year.
Thus, a dollar deposited today has a higher future value – the same is true for investments.
Future value is an important calculation because it tells investors and individuals how much investment made today (present value) will be worth in the future.
The formula to calculate FV is:
Where:=the Investment amount
=Interest rate
=number of years
An Example:
If I deposit $100 into an account earning 10% per year, how much will my deposit be worth after five years?
DATA FutureValue;
rate = 10/100;
nper = 5;
pv = -100;
pmt = 0;
fv = finance('fv', rate, nper, pmt, pv);
format rate percent7.2 pv fv pmt dollar10.2;
RUN;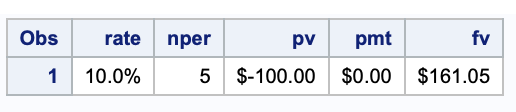
What if we had the same problem, but interest was compounded monthly?
data futurevalue;
rate = (10/100)/12;
nper = 5*12;
pv = -100;
pmt = 0;
fv = finance('fv', rate, nper, pmt, pv);
format rate percent7.2 pv fv pmt dollar10.2;
run;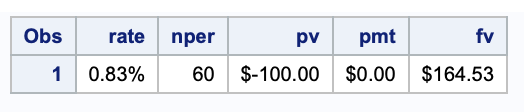
2. Future Value of an Annuity
The future value of an annuity is a way of calculating how much money a series of payments will be worth at a certain point in the future.
The formula to calculate the FV of an annuity is:
Where: =cash flow per period
=interest rate
=number of payments
An Example:
How much would I have in my retirement account if I deposited $2000 each year for 35 years and earned 10% on my savings?
data futurevalueannuity;
rate = 10/100;
nper = 35;
pmt = -20000;
fva = finance('fva', rate, nper, pmt);
format rate percent7.2 fva pmt dollar20.2;
run;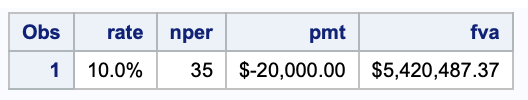
Instead, what if I made monthly deposits of $166.67?
data futurevalueannuity;
rate = (10/100)/12;
nper = 35*12;
pmt = -20000;
fva = finance('fv', rate, nper, pmt);
format rate percent7.2 fva pmt dollar20.2;
run;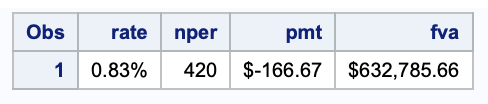
3. Calculating the Future Value of an annuity due
An annuity due is a series of equal consecutive payments that you are either paying as a debtor or as a lender.
The significant difference between an annuity due and an ordinary annuity is that payments for an ordinary annuity are made at the end of the period instead of annuity due payments made at the start of each period/interval.
An annuity due’s future value is also higher than an ordinary annuity by a factor of one plus the periodic interest rate. Each cash flow is compounded for one additional period compared to an ordinary annuity.
An Example:
How much would I have in my retirement account if I deposited $2000 at the beginning of each year for 35 years and earned 10% on my savings?
data futurevalueannuitydue;
rate = 10/100;
nper = 35;
pmt = -2000;
fv = finance('fv', rate, nper, pmt);
fvad = fv * (1+rate);
format rate percent7.2 fv fvad pmt dollar20.2;
run;
Instead, what if I made the beginning of the month deposits of $166.67?
DATA FutureValueAnnuityDue;
rate = (10/100)/12;
nper = 35*12;
pmt = -166.67;
fv = finance('fv', rate, nper, pmt);
fvad = fv * (1+rate);
format rate percent7.2 fv fvad pmt dollar20.2;
RUN;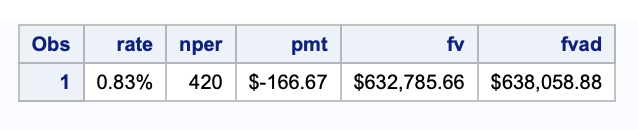
4. Calculating Present Value
It refers to a concept called “the time value of money “. Consider an example —if you were given $1 today, it is worth more than the same $1 five years from now. This is due to the changing value of money and inflation and the potential of money to earn interest from other investments.
The formula to calculate PV is:
Where: = Present Value
= Future Value
=interest rate
=number of periods
An Example:
How much would I need to deposit today in an account earning 10% per year to accumulate $10,000 after five years?
DATA FutureValue;
rate = (10/100)/12;
nper = 5*12;
pv = -1000;
pmt = 0;
fv = finance('fv', rate, nper, pmt, pv);
format rate percent7.2 pv fv pmt dollar10.2;
RUN;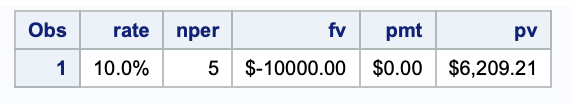
What if my interest was compounded monthly?
data presentvalue;
rate = (10/100)/12;
nper = 5*12;
fv = -10000;
pmt = 0;
pv = finance('pv', rate, nper, pmt, fv);
format rate percent7.2 pv fv pmt dollar10.2;
run;
5 . Present Value of an Annuity
The present value of an annuity measures how much money will be required to produce a series of future payments.
The formula to calculate the PV of an annuity is:
where: =cash flow per period
=interest rate
=number of payments.
In this example, we still look at the loan, but this time we want to know how much we can borrow for a home if we repay the loan with $12,000 per year for the next 30 years at an 8% interest rate.
data presentvalueannuity;
rate = 8/100;
nper = 30;
pmt = -12000;
pva = finance('pv', rate, nper, pmt);
format rate percent7.2 pva pmt dollar20.2;
run;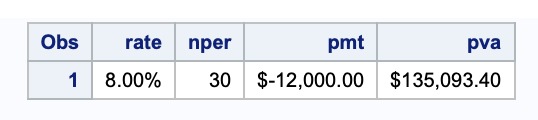
What if I wanted to know my monthly payments for a $20,000 car loan over five years at 8%?
data presentvalueannuity;
rate = 8/100;
nper = 30;
pmt = -12000;
pva = finance('pv', rate, nper, pmt);
format rate percent7.2 pva pmt dollar20.2;
run;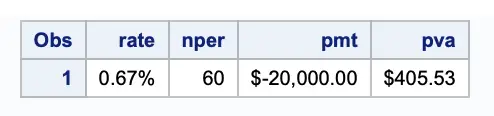
6. Present Value of an Annuity Due
The present value of an annuity due (PVAD) calculates the value at the end of the number of periods given, using the current value of money.
For example, you could use this formula to calculate the present value of your future rent payments as specified in your lease. Let us say you pay $1,000 a month in rent.
Below, we can see what the next five months would cost you, in terms of present value, assuming you kept your money in an account earning 5% interest.
data presentvalueannuitydue;
rate = 5/100;
nper = 5;
pmt = -1000;
pva = finance('pv', rate, nper, pmt);
pvad = pva * (1+rate);
format rate percent7.2 pva pmt dollar20.2;
run;
7. Computing the number of periodic payments we have to make.
What about the number of payments you need to make to pay back $1500 with $68 per month?
We use the same setup as before, but this time we set the FINANCE() function to calculate nper.
data nper;
rate=(8/100)/12;
pmt=-68;
pv=1500;
fv=0;
nper=round(finance('nper', rate, pmt, pv, fv));
format rate percent7.2 pv fv pmt dollar10.2;
run;
So we have to make 24 payments to pay back $1500 over 2 years.
8. What is the annual interest?
Now we want to look at the yearly interest rate when you pay back a loan of $1500 with 24monthly payments of $68.
The result from the FINANCE() function is the monthly interest. Therefore, you have to multiply the result by 12 to get the annual interest rate.
data rate;
nper=24;
pmt=-68;
pv=1500;
fv=0;
rate=finance('rate', nper, pmt, pv, fv) * 12;
format rate percent7.2 fv pv pmt dollar20.2;
run;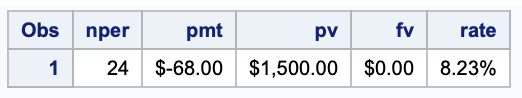
9. The Effective Annual Interest Rate
The effective annual interest rate is the actual return on a savings account or any interest-paying investment when the effects of compounding over time are considered.
It also shows the real interest on a loan, a credit card, or other debt.
For example, consider these two investment offers:
Investment A pays 10% interest, compounded monthly. Investment B pays 10.1% compounded semi-annually. Which is the better offer?
In both cases, the interest rate shown to you is the nominal interest rate.
The effective annual interest rate is calculated by adjusting the nominal interest rate for the number of compounding periods the financial product will experience.
In this case, that period is one year.
The formula and calculations are as follows:
where: = Nominal Interest Rate
$latex n$=Number of compounding periods
In SAS, you can use the FINANCE function as below.
data investments;
rate_a=10/100;
nper_a=12;
rate_b=10.1/100;
nper_b=2;
effect_in_a = finance('effect', rate_a, nper_a);
effect_in_b = finance('effect', rate_b, nper_b);
format rate_a rate_b effect_in_a effect_in_b percent10.2;
run;
- For investment A, this would be:
10.47% = (1 + (10% / 12)) ^ 12 - 1 - And for investment B, it would be:
10.36% = (1 + (10.1% / 2)) ^ 2 - 1
Investment B has a higher stated nominal interest rate, but the effective annual interest rate is lower than the effective rate for investment A. This is because Investment B compounds fewer times over the year.
What would be the return at the end of one year if an investor puts $5,000,000 into one of these investments?
The accumulated value of an investment can be calculated in SAS using the <a href="https://documentation.sas.com/doc/en/pgmsascdc/9.4_3.5/lefunctionsref/n0ledxl0wyn9jyn12hi34nlpp7ve.htm">COMPOUND</a> function.
data returns;
investment_A=compound(5000000, ., 0.1/12, 12);
investment_B=compound(5000000, ., 0.101/2, 2);
Diff=investment_A-investment_B;
run;Output:
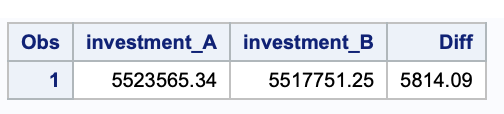
Note that the second argument has been set to missing, which indicates that the future amount is to be calculated. The 10% Effective Interest Rate has been converted to a monthly rate of 0.1/12 and 10.1% to 0.101/2.
The rate argument is the fractional (not the percentage) interest rate per compounding period. As you can see, the wrong decision would cost more than $5,800 per year!!.
10. Net Present Value (NPV)
Net present value is the present value of the cash flows at your project’s required rate of return compared to your initial investment.
The Net Present Value (NPV) is a method that is primarily used for financial analysis in determining the feasibility of investment in a project or a business. It is the present value of future cash flows compared to initial investments.
Today’s cash is more valuable than the cash we will receive after five years due to inflation.
Hence, when you decide to invest money each year, you must first check how much that money is worth today. This is called the net present value of money.
|
Period
|
Project A | Discount rate | ||
| 0 | $ (8,000.00) | 18% | ||
| 1 | $ 3,400.00 | 18% | 3411/(18%+1)^n = | $ 2,881.36 |
| 2 | $ 4,000.00 | 18% | 4070/(18%+1)^n = | $ 2,872.74 |
| 3 | $ 5,000.00 | 18% | 5824/(18%+1)^n = | $ 3,043.15 |
| 4 | $ 3,000.00 | 18% | 2965/(18%+1)^n = | $ 1,547.37 |
| Total Cash Flow | $ 15,400.00 | |||
| Present Value Of Cash Inflows (PVIFA) | $ 10,344.61 | |||
| Net Present Value (NPV) | 10344+(-8000) = | $ 2,344.00 |
|
As you can see, at the end of the 5th year, the NPV is $2344. It can be calculated in SAS as below.
data NPV;
rate=0.18;
investment=-8000;
year1=3400;
year2=4000;
year3=5000;
year4=3000;
npv=finance('npv', rate, year1, year2, year3, year4)+investment;
format rate percent7.2 year1-year4 investment npv dollar20.2;
run;Output:
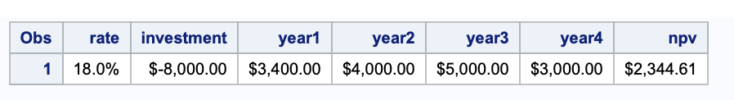
Note. If your cash flows are not periodic, use the XNPV function.
11. Computing the internal rate of return (IRR) for a series of cash flows
The internal rate of return is a metric used in financial analysis to estimate the profitability of potential investments.
The internal rate of return is a discount rate that makes all cash flows’ net present value (NPV) equal to zero.
The present value of money is always higher than the same amount in future. This is due to uncertainty in the interim period and price inflation, which reduces your purchasing power.
Any future value (FV) of money must be “discounted” or reduced at some discounting rate to arrive at its present value (PV). However, any amount in the present need not be discounted.
where
is the discounting rate
is the discounting period (usually years)
We will use the previous example to calculate the IRR of the investment.
data npv;
rate=0.18;
investment=-8000;
year1=3400;
year2=4000;
year3=5000;
year4=3000;
irr=finance('irr', investment, year1, year2, year3, year4);
format irr percent7.2 year1-year4 investment dollar20.2;
run;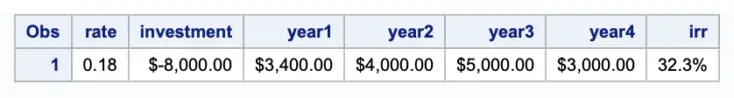
Output:
That was all we had to say about financial functions. In SAS, you can use FINANCE() for all the calculations. If you know of any other functions in SAS, do let us know in the comments.
We hope you have enjoyed the article, and we will look forward to writing more articles on SAS.





My brother recommended I may like this web site.
He was once totally right. This publish actually made my day.
You can not imagine simply how a lot time I had spent for this info!
Thank you!